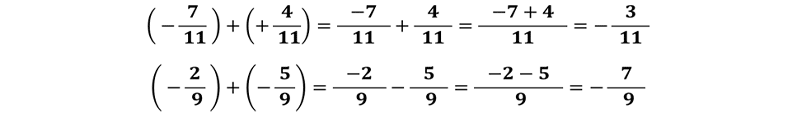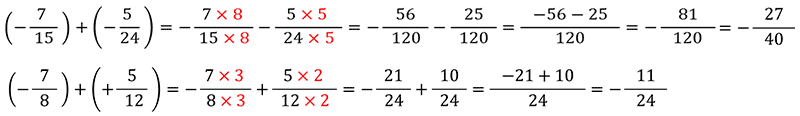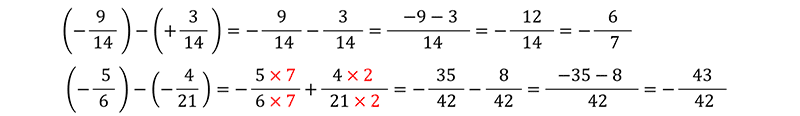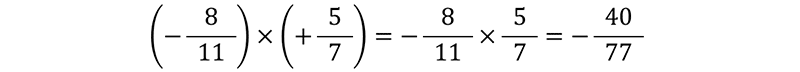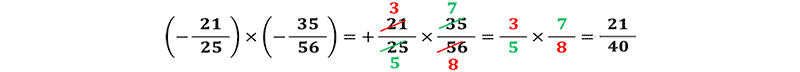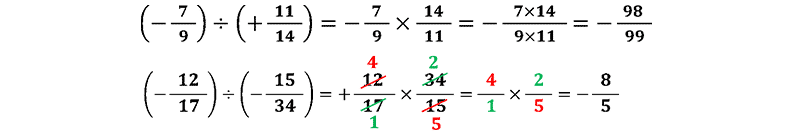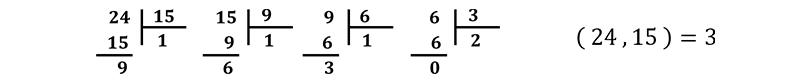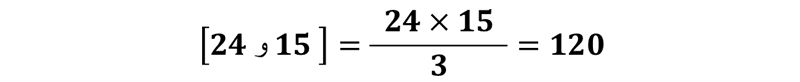در مقاله آموزش چهار عمل اصلی اعداد گویا به بررسی چهار عمل اصلی ریاضی یعنی جمع ، تفریق ، ضرب و تقسیم برای عددهای گویا یا عدد کسری می پردازیم. همچنین در این مقاله به آموزش بزرگ ترین شمارنده مشترک و کوچک ترین مضرب مشترک عددها اشاره می کنیم .

جمع عدد گویا

روش اول، به کمک محور اعداد

در روش اول برای جمع عدد کسری ابتدا عدد گویای اول را روی محور مشخص می کنیم و از آن به اندازه ی عدد گویای دوم ( با توجه به مثبت و یا منفی بودن ) روی محور حرکت می کنیم تا حاصل بدست آید.

روش دوم

در این روش برای بدست آوردن حاصل جمع عداد گویا ابـتدا با برداشتن پرانتز ها مختصر نویسی می کنیم.

آ) اگر دو کسر دارای مخرج مساوی باشند:

برای بدست آوردن حاصل  جمع، مخرج مشترک را نوشته و سپس صورت ها را مانند عددهای صحیح با هم جمع می کنیم.

ب) اگر دو کسـر دارای مخرج مساوی نباشند:

دو کسر را با استفاده از کوچکترین مضرب مشترک مخرج ها، هم مخرج می کنیم. سپس برای بدست آوردن حاصل مخرج مشترک را نوشته ، صورت ها را مانند عددهای صحیح جمع می کنیم.

تفریق عدد های گویا

برای بدست آوردن حاصل تفریق عدد گویا، ابتدا تفریق را به جمع تبدیل می کنیم، به این ترتیب که عدد اول را می نویسیم و به جای تفریق (یعنی علامت منها)، یک علامت جمع (یعنی علامت بعلاوه) قرار می دهیم و عدد دوم را قرینه می کنیم. سپس مانند جمع عمل می کنیم. به عبارت دیگر ، برای بدست آوردن حاصل تفریق، عدد گویای اول را با قرینه عدد گویای دوم جمع می کنیم.

ضرب عدد گویا

برای محاسبه ضرب دو عدد گویا ابتدا مانند ضرب عددهای صحیح علامت حاصلضرب را تعیین می کنیم و سپس صورت را در صورت ضرب و حاصل صورت را بدست می آوریم و مخرج را در مخرج ضرب کرده حاصل مخرج را بدست می آوریم.

نکتــه مهم: بهتر است در صورت امکان کسرها را ساده کنیم.

تقسیم عدد های گویا

برای بدست آوردن حاصل تقسیم عددهای گویا یا عدد کسری، ابتدا مانند تقسیم عددهای صحیح علامت حاصل را تعیین می کنیم . سپس کسر اول را در معکوس کسر دوم ضرب می کنیم. [یعنی کسر اول را می نویسیم و به جای تقسیم ، علامت ضرب را قرار می دهیم و کسر دوم را معکوس می کنیم.]

در ادامه ایم مقاله با توجه به لزوم تعیین مخرج مشترک در جمع و تفریق کسرها ، به یادآوری روش تعیین بزرگترین شمارنده مشترک و کوچکترین مضرب مشترک عددها اشاره می کنیم.

روش بدست آوردن بزرگترین شمارنده مشترک دو عدد (ب . م . م – بزرگترین مقسوم علیه مشترک)

     آ ) ابتدا عدد بزرگتر را بر عدد کوچکترتقسیم می کنیم . اگر بخش پذیر بود، عدد کوچکتر( یعنی مقسوم علیه این تقسیم ) بزرگترین مقسوم علیه خواهد بود.

    ب) اگر شرایط الف برقرار نبود و تقسیم باقیمانده داشت . مقسـوم علیه تقسیم مرحله قبل را بر باقیمانده تقسیم می کنیم و شرایط مرحله قبل را بررسی می کنیم.

    پ) این عمل تقسیم را ادامــه می دهیم تا به تقسیمی برسیم که باقیمانده آن صفر باشد ، مقســوم علیه آخرین تقسیم بزرگترین مقسوم علیه مشترک می باشد.

مثال: بزرگترین مقسوم علیه مشترک دو عدد 15 و 24 را بدست آورید.

روش بدست آوردن کوچکترین مضرب مشترک دو عدد (ک . م . م – کوچکترین مضرب مشترک)

برای بدست آوردن کوچکترین مضرب مشترک دو عدد ، حاصل ضرب دو عدد را بر بزرگترین مقسوم علیه مشترک آن ها تقسیم می کنیم .

مثال : کوچکترین مضرب  مشترک دو عدد 15 و 24 را بدست آورید .

شما عزیزان با مطالعه منابع و استفاده از فیلم های آموزش ریاضی، می توانید به درک دقیق مفاهیم ریاضی دست یابید.

آموزش فصل چهارم ریاضی هشتم | جبر و معادله

عزیزاله رضائی – مدرس و طراح فیلم های آموزش ریاضی